EC-Force

Introduction: Bose-Einstein condensation of Wannier-Mott (WM) excitons was predicted by Moskalenko[1], Blatt, Böer and Brandt[2] in 1962 and elaborated later by the group lead by Keldish [3]. WM excitons are hydrogen-atom like bound states of interacting electrons and holes (Fig.1.a below) itinerant within semiconductor medium and there has been a tremendous research to experimentally verify this proposal using bulk semiconductor samples [4,5]. The driving interaction of the condensation of the WM excitons is the attractive Coulomb coupling between electrons and the holes and the repulsive dipolar interaction between the excitons. However, the short lifetime of the bulk WM excitons (a few nanosecond) is insufficient for the thermal equilibrium to be reached before any condensation can take place. 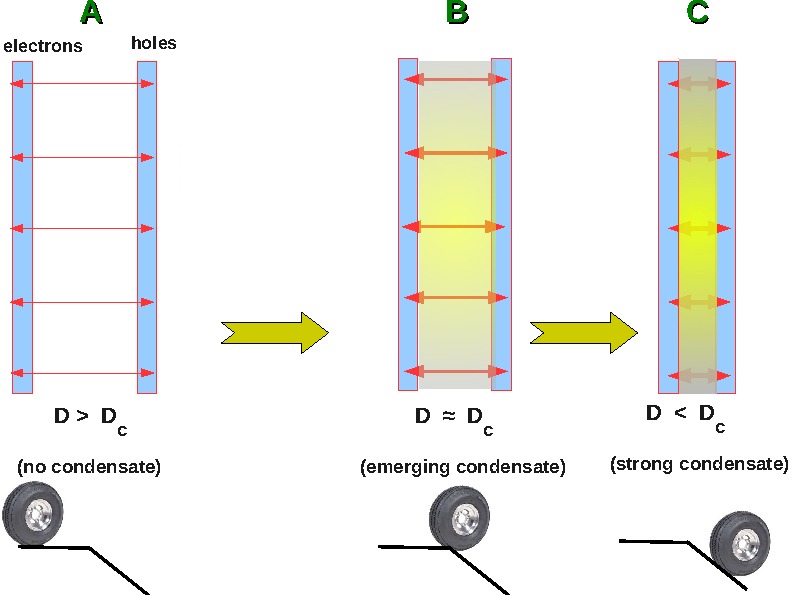Since early 90's, with the progress made in growing semiconductor heterojunctions, the search for the condensation of WM excitons is made by using spatially indirect electron-hole bands confined in different quantum wells [6] separated by a distance comparable to an exciton Bohr radius a₀ ~ 100 Å as depicted in Fig.1.b below (the double quantum well-DQW geometry). In addition to this DQW geometry, a strong external electric field is usually applied [7,8] to keep the electrons and holes away from each other by pinning their wavefunctions at the outer edges of their respective quantum wells.

More specifically, the authors investigate the Coulomb coupling between the interacting and spatially separated electron-hole system confined to two separate quantum wells, and due to the spin neutrality of the Coulomb interaction, the pairs come in all possible spin configurations as shown in Fig.1.c. There are two effects of the attractive Coulomb coupling which is a function of the distance between the electron and the hole wells. If this distance is on the order of an exciton Bohr radius a₀ the first effect of the Coulomb coupling is the formation of the electron-hole bound states, i.e. the WM exciton. Below a certain critical temperature (the critical temperature), the second effect of the Coulomb interaction comes into play. In sufficiently low densities (the critical density), when excitons act like independent bosons, they are expected to experience a phenomenon called Bose-Einstein condensation and form a phase coherent ground state, i.e. the exciton condensate (EC). In this new ground state, excitons act collectively very much like the motion of a school of small fish in the sea. This new ground state lowers the free energy of the system with the gap in energy depending on the strength of the Coulomb coupling. Due to the small exciton reduced mass, the critical temperature of the EC is on the order of a few Kelvin. As the density increases, the exciton wavefunctions start spatially overlapping, moving the electrons and the holes into a BCS like condensation.

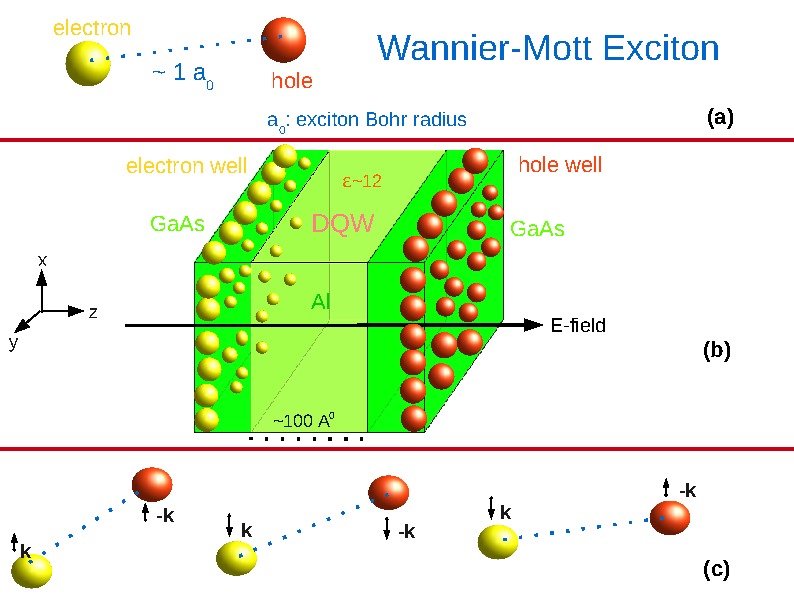
Fig.1. (a) A description of a Wannier-Mott exciton without the spin degree of freedom indicated. (b) Electron and hole quantum wells in a semiconductor DQW. Due to the external electric field the electron and the hole wavefunctions locate at the outer surfaces of the respective quantum wells, (c) Dark and bright excitons.

Symmetries and other complications: In an exciton condensate two different types of pairings are allowed between an electron in an s-like, and a hole in a p-like orbital states. The bright pairs are composed of opposite electron and hole spins combined into a bright singlet and a bright triplet, whereas the dark triplet pairs are composed of paralel electron and hole spins. In addition to these complications, the bright and the dark states are not totally independent. Coupling between the spin and the orbital degrees of freedom can also be crucially important in many of the semiconductor heterostructures. There are also fundamental symmetries such as the time reversal symmetry, spin degeneracy, orbital rotation symmetry, fermion exchange symmetry, and these play crucial role in the formation of the EC [9]. The presence or absence of these symmetries affect the interplay between the dark and the bright components and can even change the topology of the condensate in the energy-spin space. A thorough understanding of the exciton condensate (EC) has been challenging mostly due to these and other inherently experimental diffculties [10] such as the short exciton lifetime and the momentum as well as angular momentum dependence of the residual interactions between the fermionic constituents. The bright states can couple to the radiation field through the recombination and pair creation processes due to their odd total angular momenta, whereas the dark states do not couple. However, in reality, the dark and the bright states are mixed [11,12]. Two dark states can also turn into to bright ones through a mechanism called Pauli exchange scattering before coupling to the radiation field [13]. Therefore there is always a weak bright component in the ground state by which the photoluminescence experiments can be made.

Radiative corrections: Electron and hole pairs can recombine to radiate a photon, and this photon with the right energy can also create a pair, but these processes can only happen for the bright states as shown in Fig.2.b and 2.c. These radiative processes cost a positive energy which is not liked much by the other members of the condensate, i.e. the dark excitons. Therefore the bright exciton population in the ground state is dramatically suppresed in favour of the dark states [12]. Pauli scattering of two bright pairs can turn into to dark pairs whereas the reverse process is energetically disfavoured in low temperatures.

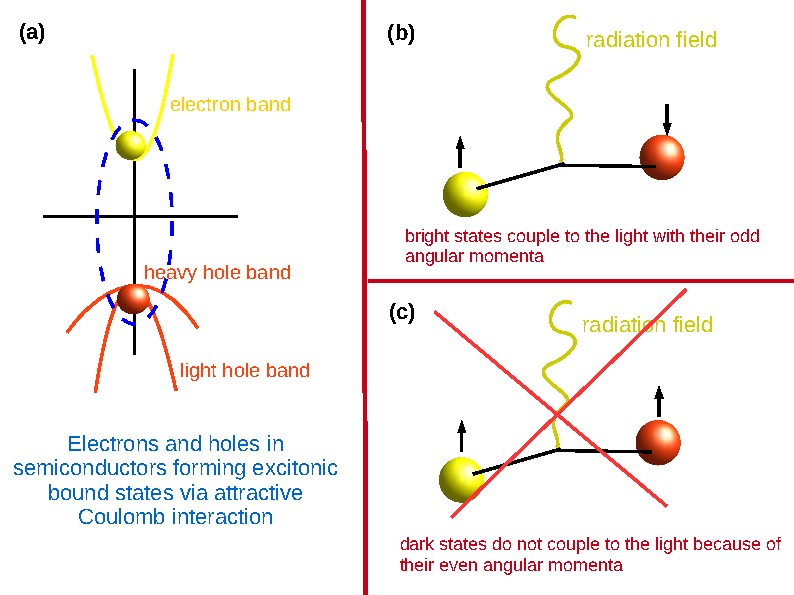
Fig.2. (a) Electron and hole bands in semiconductors forming excitons. (b) & (c) Radiation field and its coupling to the bright and dark states.

Until the recent experiment by High, Leonard, Hammack, Fogler, Butov, Kavokin, Campman and Gossard in 2012 (Ref.[14]), the photoluminescence measurements have been limited in probing all components of the condensate due to the weakness of the bright contribution. As the names suggest, bright condensates couple to the radiation field(or simply light) where as their dark counterparts do not. Since photoluminescence experiments can only probe the bright condensate, the amount of bright states in the ground state of the coherent exciton gas is essential in these experiments. Since bright contribution is strongly suppresed by the dark one, this also makes the photoluminescence experiments highly difficult. In Ref. [14] using a Mach-Zhender interference measurements, a clear evidence on the EC was established by the observation of the interference fringes. This is a clear evidence that there is a macroscopic and coherent order in the ground state, hence the condensate.

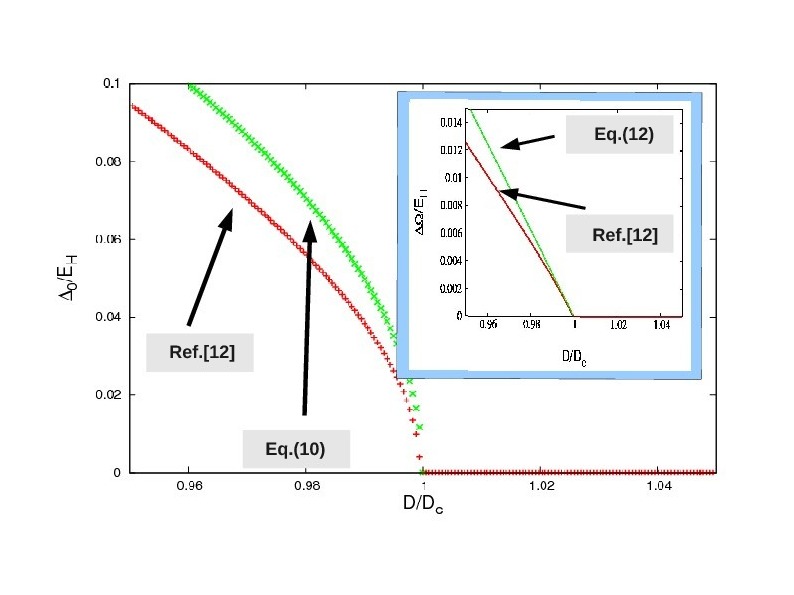
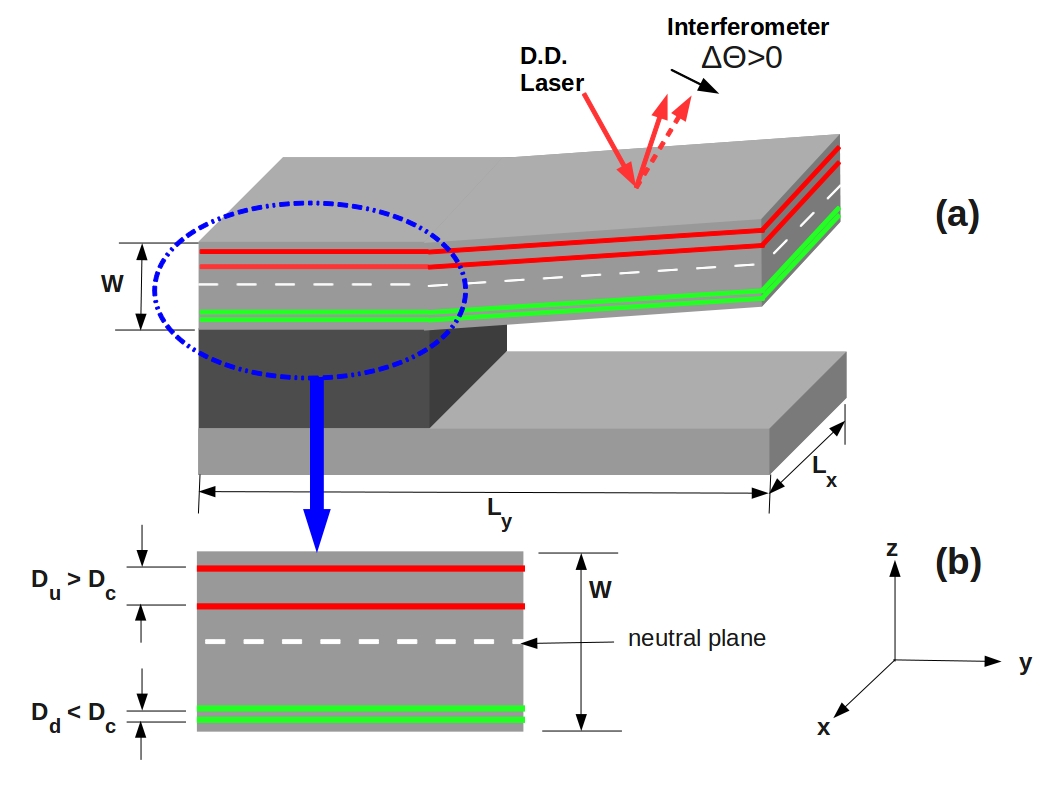
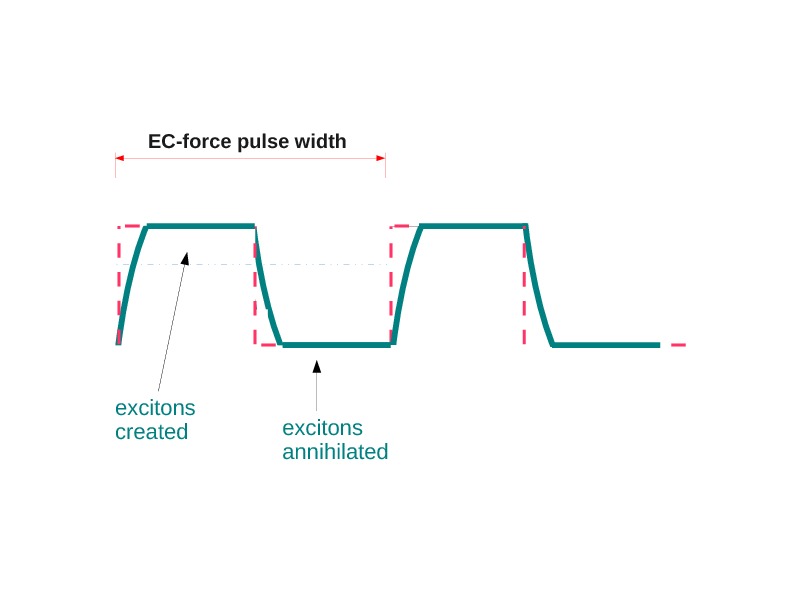
It should be realized that EC research with such theoretical and experimental challenges is an outstanding resource in better understanding the unconventional aspects of many body interacting quantum systems in general. The exciton condensate is one of the most difficult examples in condensed matter physics where a variety of different mechanisms and unconventional examples of pairings play leading role all at the same time. It is a common sense to say that, in such a broad area, new effects unknown in other systems should also be expected. In this work, the authors demonstrated that the Coulomb interaction between electrons and holes in the presence of the exciton condensate gives rise to a conceptually new and nonlocal force, which they coined as the EC-force, of which observation is expected not only to shed light on the theoretical and experimental understanding of the EC but also stimulate a broader research on other many body systems where similar effects can arise.

EC-force is a fundamentally new effect in condensed matter physics: In their earlier numerical calculations [12], taking into account all manifested symmetries a well as the radiative couplings, the authors noticed that, the change in ground state energy of the EC with respect to the distance between the electron and the hole quantum wells has a discontinuity at a critical distance between the electron and the hole quantum wells (left figure in Fig.3 below). This sharp discontinuity is actually a boundary which separates the normal excitonic liquid from the condensed excitons. This picture is very much like a perfectly smooth street with a huge hole in it. As a wheel is very slowly moved towards the hole, it suddenly rushes into the hole, the normal excitonic liquid becomes unstable as it enters the boundary and wants to go to lower energies and condense stronger (Fig.3 with stages A,B, C below). As the electron and the hole wavefunctions are pinned by the strong external electric field, the attempt to go to lower energies results in forcing the distance to be narrowed between the electron and the hole quantum wells. This clearly indicates a new kind of force, purely due to the dependence of the condensate's energy on the distance between the electron-hole quantum wells, i.e. the EC-force.

Fig.3. On the left is the solution of the energy gap as a function of the distance between the layers and the exciton concentration (Adopted from Ref.[12]). The positions indicated by A,B and C correspond to different distances between the electron and the hole quantum wells. On the right, (A) is the absence of condensation for D > D_c , (B) emerging condensate for D ~ D_c , and (C) a strong condensate for D < D_c with D_cas the critical distance. The right arrows in green indicate the direction of lowering the free energy. The wheel and the hole analogy used in the text is also described.

In attempt to understand this, the authors succeeded in devicing tools reproducing this effect analytically which then lead them into a mathematical expression for the EC-force [15]. This new force is strong at the point where the discontinuity occurs but is present and relatively constant at all distances smaller than the critical distance (like the wheel going down a constant slope once it enters the hole). The dependence of the energy gap as well as the free energy on the distance between the quantum wells is shown in Fig.4 below. The agreement between the numerical calculations and the analytic model is remarkable. The EC-force is proportional to the slope of the green curve in the inset of Fig.4. The calculations show that for a typical exciton concentration of 10¹¹ cm^-2 the strength of this force is tiny (but not tinier than that cannot be measured!), i.e. approximately 10^-9 Newtons.

Fig.4. The main figure depicts the energy gap as the electron-hole well distance D is varied (normalized with respect to the critical distance D_c). The inset is the same for the free energy. The red dots indicate our earlier numerical calculations in Ref.[12] whereas the green dots depict the analytical calculations in Ref.[15] (This figure is taken from Ref[15]. The reference and equation numbers therein are inapplicable here.)

The recently obtained clear evidence[14] for the existence of exciton condensate is also a promise for the experimental observation of this new effect. Although EC-force is reminiscent of the electromagnetic Casimir force [15], these two forces are also significantly different. Standard Casimir force is caused by the existence of electromagnetic boundaries and fluctuations of the electromagnetic field in the vacuum. EC-force is fully driven by the excitonic condensate and appears due to the spatial dependence of the free energy via the Coulomb interaction.

Fig.5. (left) (a) The depiction of the proposed experimental setup. (b) Zoomed view of the two DQWs. (This figure is taken from Ref[15]). Typical dimensions of the cantilever are L_x=10 µm , L_y=100 µm and W=0.3µm.
Fig.6. (right) Appearance of the EC-force as a function of time follows the exciton creation and annihilation pattern indicated by green lines. Ignoring the typically 1 µs lifetime of the excitons, the generated EC-force follows the pulse profile stimulated by the driving laser. The frequency of the pulse also coincides with the mechanical resonance frequency of the cantilever (nearly 10-20 kHz range).

An experimental proposal to measure the new effect: There may be various other proposal deviced by experimental groups to measure the EC-force in the future. Here one can discuss a basic experimental proposal to measure this effect. Due to the existing strong Coulomb force as well as the dielectric between the quantum wells, the direct measurement is much more challenging than measuring the electromagnetic CF between the two metallic plates separated by vacuum. Recently, Yamaguchi, Okamoto, Ishihara, and Hirayama [16] have detected the motion of a micromechanical oscillator with an amplitude on the order of 50nm. Here, upon [16], the authors use the EC-force as the driving force of the micromechanical oscillator as shown in Fig.6.

The growth process and the production of the sample in Fig.(4) is paralel to [16]. The idea is to grow two GaAs DQW structures depicted by the green and the red lines respectively in Fig.(5) both below and above the neutral plane of the Al_xGa_1-xAs type micromechanical cantilever. The DQWs are then populated by electrons and holes using a resonant pump laser in the presence of an external electric field and at a temperature much less than the critical temperature to condense the excitons. The upper DQW is in the uncondensed regime incidated by (A) in Fig.3. The lower DQW is in the condensed regime indicated by (C) in Fig.(3), therefore the EC forms within a few nanoseconds after thermalization of the electrons and holes with the lattice in the lower DQW. According to their prediction, the EC-force should then be simultaneously generated with the appearance of the condensate in the lower DQW. The formation of the EC-force in the lower DQW follows the same pattern as the creation and the annihilation of the excitons as indicated in Fig.6. The internal stress created by the EC-force becomes the driver of the mechanical oscillations at the mechanical resonance frequency of the cantilever. The oscillations of the resonating cantilever and the deflection angle depicted in Fig.5 can be measured by a second laser (the deflection detection-DD laser in Fig.5). Interested reader can find more details of the experimental proposal as well as a discussion of the secondary effects in Ref.[15].

What does a force due to an Exciton-Condensate mean?: The EC-force is a nonlocal force like the Casimir force between two metallic plates held in vacuum [17]. However, this is the only similarity between these two effects. A measurable force emerging due to the formation of a condensate is an unique effect of its own right and the experiments to measure this phenomenon are within reach and possible which may find other analogies in low temperature condensed matter physics. Bose-Einstein atomic condensates are difficult to measure this force due to the strongly local interactions between the atoms. However, one possible candidate is the topological exciton condensate in which the Dirac-cone states pinned at the top and the bottom surfaces of a topological insulator filled with electrons and the holes are coupled through the Coulomb interaction.

*This presentation aforementioned here is based on some of the progress made in references [12] and [15] and is, by no means, meant to be a review of the whole progress in the entire field.